L’estimation des probabilités lors d’une évaluation des risques

L’évaluation des risques se fait sur deux facteurs : la vraisemblance ou la probabilité d’occurrence d’un événement (généralement adverse) et la magnitude d’impact associé à celui-ci. Le terme vraisemblance est souvent utilisé pour estimer qualitativement les événements, c’est-à-dire en utilisant des catégories (faible, moyen, élevé) ou des valeurs ordinales (1, 2, 3, 4) reliées entre elles et servant à les hiérarchiser. On lit parfois que le fait d’utiliser des nombres pour les hiérarchiser (les rangs) et effecteur des calculs (addition, multiplication ou moyenne) rend la méthode quantitative mais c’est un abus de langage. Pour qu’on puisse parler de méthode quantitative, il faudrait que les calculs aient un sens mathématique précis, or multiplier ou additionner des rangs n’en a aucun. Un rang est comparé à un autre rang, mais ne signifie pas grand-chose dans l’absolu. Il est absurde de le multiplier à une valeur d’impact si les valeurs ne sont pas strictement quantitatives et pas seulement numériques. En dehors de ce cas précis, l’expression mathématique multipliant les valeurs ordinales des deux critères n’a qu’une portée pédagogique : il met l’accent sur le fait que si l’un des facteurs est nul, le niveau de risque serait également nul …

La vraisemblance fait référence à la plausibilité qu’un certain événement se produise, quand on juge celui-ci vraisemblable ou pouvant se produire sous certaines conditions. Pour estimer les chances qu’un certain événement puisse se produire, en espérant aller au-delà d’un vague sentiment qui peut comprendre beaucoup de biais potentiels, on estime sa probabilité afin de rendre l’évaluation plus objective. Les probabilités sont utiles à quantifier (avec plus ou moins d’exactitude) le niveau d’incertitude (et donc du risque).

L’objectif de toute analyse de risque sérieuse est de n’envisager que des informations pertinentes et les plus exactes possibles, sans tomber dans les spéculations spécieuses qui sont la marque des analyses de très mauvaise qualité. Mais est-ce que l’utilisation des probabilités rend l’évaluation plus objective et plus exacte ? Et quel est leur réel intérêt ? Quelles techniques probabilistes utiliser et pour quoi faire ? Nous allons tenter de répondre à ces questions dans cet article. Gardez à l’esprit que si mon intérêt pour les risques m’a porté de force vers ce sujet crucial de la quantification des risques, je suis issu d’une formation littéraire. Les scientifiques me pardonneront tout raccourci ou approximation et ils sont invités à me corriger.

Première chose à clarifier, il existe deux manières d’estimer des probabilités :

• La méthode dite objective et autrement appelée fréquentiste, car utilisant l’estimation des fréquences d’un événement
• La méthode dite subjective et autrement appelée bayésienne (de son découvreur Bayes).

Dans la méthode fréquentiste, on estime le nombre des cas favorables (l’événement étudié se produit) par rapport au nombre des cas possibles pour un événement quelconque, tous les cas possibles étant supposés également possibles (il y a autant de chances qu’un événement A, B ou C se produisent). C’est le fameux tirage de dés non truqués : il y a normalement une chance sur 6 (un dé classique possède 6 faces) que n’importe quelle valeur soit obtenue à chaque lancer, l’issue étant indépendante de l’observateur. Plus important, les lancers sont des événements distincts et sans aucune relation entre eux. Ces conditions sont importantes car elles définissent le sens du mot aléatoire en probabilités, ce qui a des implications directes avec son utilisation dans l’évaluation des risques.

Il faut ouvrir une parenthèse importante : il est fréquent de lire ou d’entendre les termes aléatoire et incertain comme s’ils étaient interchangeables. Or, il faut comprendre aléatoire comme se rapportant à l’observateur et à son incapacité à prédire les issues possibles à l’avance, à sa passivité relativement à l’événement dont il ne peut influencer l’issue. Cet événement est imprévisible (pour lui), mais on considère a priori que les issues possibles ont toutes une chance de se produire. On comprend de suite qu’un événement aléatoire est forcément incertain, mais est-ce que tous les événements incertains sont aléatoires et le fruit du hasard ?
Un événement incertain est également difficilement prévisible même s’il n’est pas complètement le fruit du hasard. Il est fonction de paramètres qui ne sont pas ou mal connus. C’est notamment le cas d’un événement composé d’un nombre élevé de paramètres qui ne sont pas tous maîtrisables ou d’une absence de données pour tirer des conclusions définitives. C’est aussi le cas pour tous les événements associés à un choix humain pas toujours prévisible.

Selon les explications précédentes :

• Un événement cyber accidentel dû à un dysfonctionnement matériel mal maintenu est-il un événement aléatoire ou seulement incertain ?
• Un événement cyber intentionnel à la suite d’une attaque complexe dont l’origine est un cybercriminel, est-il aléatoire ou seulement incertain ?

Ces questions sont importantes car elles déterminent quelles techniques probabilistes sont utiles dans chaque cas et, surtout, les leurs limites pour estimer un événement de manière pertinente.

Les probabilités objectives ou fréquentistes

 Avec la méthode fréquentiste, on se fait l’observateur objectif des différents lancers. On peut ainsi réaliser 100 lancers de dés, observer les résultats et estimer les fréquences d’obtenir tel événement ou tel autre qui seront rapportées. On ne tient compte d’aucun autre paramètre pouvant influencer le résultat, c’est une des conditions d’utilisation de cette méthode.
De la même manière, on peut observer et noter toutes les attaques cyber résultant d’une méthode particulière, sans se soucier des motivations et de la foule de paramètres autour de ces attaques (intentionnelles), et ainsi obtenir la fréquence ou la prévalence de ces méthodes d’attaques. Ces chiffres sont importants lorsqu’on réalise une veille de cybersécurité. C’est la principale source permettant d’évaluer le niveau de risque inhérent (indépendamment de possibles facteurs d’atténuation) à un événement de menace (attaque).

En langage probabiliste, pour un événement A, on note cette probabilité P(A) dont la valeur se situe entre 0 et 1, avec 0 l’événement est impossible et 1 l’événement est certain.

Pour un dé possédant 6 faces numérotées de 1 à 6 : le nombre total d’issues possibles (ou « l’univers des possibilités » est l’ensemble des nombres : 1, 2, 3, 4, 5, 6. Soit 6 éléments en tout.

Les probabilités ou les chances d’avoir une issue favorable pour un événement A seront toujours estimées sous la forme d’une proportion du nombre d’issues favorable, noté n(A) sur le nombre total de possibilités, noté N. Pour le cas du dé, N = 6. On décrit ensuite l’événement que nous souhaitons estimer, par exemple :

• Les probabilités d’obtenir un 6 à chaque lancer : P(A) = 1/6  = 0,166 ou 16,67%
• Les probabilités d’obtenir un nombre impair (soit 1, 3 ou 5) P(A) = 3/6 = ½ = 0,5 = 50%

Dans le premier cas nous avons 16,67% de chances d’obtenir un 6 à chaque lancer et dans le second, on a 50% de chances d’obtenir un nombre impair.
L’exemple du dé est important : toutes les faces ont les mêmes probabilités d’apparaître ET chaque lancer est indépendant des précédents (sinon la première condition serait fausse).

Lorsqu’on estimer les fréquences des différentes attaques (approche fréquentiste) on traite les événements comme étant indépendants les uns des autres et comme le fruit du hasard. Or, il n’en est rien : si l’issue d’une attaque ou leur simple occurrence est incertaine par la méconnaissance des motivations de chaque acteur et leur ciblage, celle-ci n’est pas aléatoire. Pour compenser cette approche un peu naïve, certains experts amateurs de criminalistique ou issus du monde militaire ont tenté d’évaluer les acteurs par le biais de leurs motivations et ressources, en gros leurs MOM (Motivation – Opportunité – Moyens). Sous sa forme basique, on modélise ces acteurs sous la forme qualitative ou semi-quantitative.

Dans l’exemple ci-dessous, je vais encore utiliser une distribution normale sur 4 critères pour faire correspondre avec des niveaux qualitatifs (0 ; 0,25 ; 0,50 ; 0,75 ; 1) :

Type d’acteur	Motivation	Opportunité	Moyens	Probabilité
Cyberdélinquant	2. Modérée / 0,5	2. Modérée / 0,5	1. Faible / 0,25	2. Modérée / 0,41
Cybervoleur	3. Élevée / 0,75	1. Faible / 0,25	3. Faible / 0,25	2. Modérée / 0,41
Cybersoldat	4. Très élevée / 1	3. Élevée / 0,75	4. Très élevé / 1	4. Très élevée / 0,91

Dans cet exemple on utilise juste 3 paramètres (MOM), le plus fluctuant étant celui de l’opportunité qui revient un peu à évaluer une certaine forme de prédisposition, mais il est possible d’en ajouter beaucoup d’autres pour tenter de compenser son simplisme. Mais ça n’enlèvera pas ses défauts intrinsèques :

• On connaît rarement le type d’acteur en cause après coup, l’attribution est souvent compliquée, c’est encore plus difficile d’anticiper ;
• Le modèle est figé, les mêmes valeurs se répèteront pour chaque événement, les valeurs sont relativement absolues et étant associées à chaque catégorie d’acteur ;
• De quelle probabilité s’agit-il : d’une occurrence d’attaque ou du succès d’une attaque ? Les valeurs ne seraient pas les mêmes dans un cas ou dans l’autre ;
• L’estimation se base sur du gros bon sens et parfois sur des statistiques assez vagues, ça ne les rend pas pour autant exactes ;
• Selon l’évaluation, la probabilité qu’une attaque soutenue par un État (que j’appelle cybersoldat) serait presque certaine, ce qui ne correspond pas si on ne modère pas par d’autres critères.

Comme souvent lorsqu’on essaye d’estimer un événement incertain, on se rassure en pensant que les paramètres pris en compte et leur évaluation, même approximatifs et simplistes, c’est mieux que de ne rien prendre en compte du tout et de considérer que cela est le fruit du hasard. Mais est-ce vraiment le cas ? J’ai personnellement des doutes.

La méthode FAIR, à partir d’un certain niveau de granularité, utilise cette méthode appelée « Capacité de la menace » censée déterminer la susceptibilité à une attaque. Je la trouve archaïque et peu pertinente même si elle est drapée d’une approche mathématique qui semble faire du sens. D’ailleurs Jack Jones dit lui-même dans son livre qu’il utilise rarement ce niveau de granularité à cause de l’absence de consensus sur le mode d’évaluation …

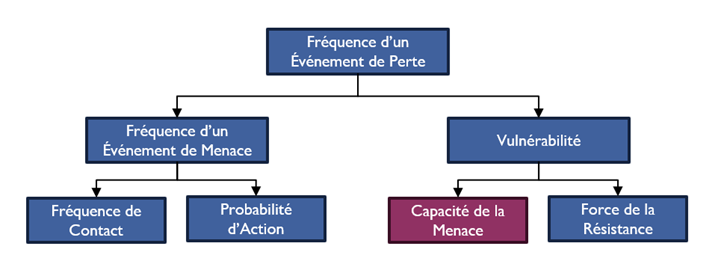
Peut-être qu’un jour nous disposerons de données statistiques abondantes et exactes, donc exploitables, mais pour l’instant la seule chose que l’on puisse raisonnablement avancer se rapporte à la typologie des attaques :

• Les attaques opportunistes sont les plus nombreuses avec un impact limité
• Les attaques ciblées sont les moins nombreuses mais leur impact peut être considérable

Peut-on mettre ça sous forme de formule ? Peut-être, en appliquant de manière un peu péremptoire un rapport respectif de 80/20 : considérons qu’environ 80% des attaques seront opportunistes et leur impact sera limité (faible à modéré) et 20% seront ciblées et leur impact sera significatif (disons élevé à très élevé). Parmi les attaques ciblées on pourrait avoir un rapport aussi 80/20 comme suit : 80% des attaques seront d’origine externe et 20% d’origine interne, avec l’idée derrière d’identifier un black swan (un événement rare mais particulièrement impactant). Les acteurs internes, si le processus d’embauche est efficace, seront probablement et majoritairement respectueux des règles déontologiques et craindront les conséquences s’ils se font attraper (appétit au risque faible, dirait-on) et ce, même s’ils possèdent des permissions étendues sur les systèmes. Les négligences sont plus fréquentes au sein des organisations que des actes revanchards d’un employé mécontent. Et si on a tous un cas ayant défrayé la chronique ces dernières années, on l’évaluerait probablement à quoi, un incident tous les dix, quinze ou vingt ans dépendant du secteur d’activité de l’entreprise et du pays.

C’est là que la méthode FAIR est intelligente et prévoit un critère appelé « probabilité d’action » ou « probabilité de passage à l’acte » qui vient modérer à la hausse ou à la baisse la modélisation MOM. Dans l’exemple précédent, on pourrait considérer que la « valeur » associée à l’organisation étudiée serait faible car située dans une région et appartenant à un secteur d’activité dont on a des statistiques montrant une faible activité.

Tout ce que nous avons vu jusqu’ici se rapporte à l’évaluation du risque inhérent. Nous n’avons pas ou très peu pris en compte les facteurs de prédisposition (ma terminologie) ou susceptibilité (FAIR) à une attaque, et particulièrement les contre-mesures éventuellement en place. Selon ma taxonomie, on doit considérer deux types de facteurs de prédisposition PEST(I)LE :

• Facteurs politiques : quelle est la probabilité que la politique menée par notre pays puisse conduire à des attaques cyber dont nous serions la cible ?
• Facteurs économiques : à quel point notre organisation évolue dans un secteur compétitif ?
• Facteurs sociaux : à quel point la politique interne à l’entreprise est susceptible de conduire à un mécontentement des employés ?
• Facteurs technologiques : à quel point la technologie que nous utilisons est susceptible d’être la cible d’attaquants ?
• Facteurs informationnels : à quel point les attaquants s’intéresseraient à nos informations et lesquelles, dans quel but ?
• Facteurs légaux et réglementaires : est-ce que notre organisation est sujette à des contraintes réglementaires dont la conformité pourrait être volontairement mise à mal par les attaquants ?
• Facteurs environnementaux : à quel point l’organisation est affectée par les phénomènes climatiques, géologiques ou écologiques ?

Au final, quel que soit le nombre et le type de critères que vous voulez examiner, l’objectif est toujours d’estimer une fréquence, soit inhérente, observée/constatée, après coup ou bien anticipée. Dans les évaluations de risques c’est ce sont les fréquences anticipées qui nous intéressent. Si vous vous rappelez du calcul de l’ALE (Annual Loss Expectancy) abordée lors d’un précédent article, la formule considère l’ARO (Annual Rate of Occurrence) multiplié par les pertes anticipées pour un seul événement ou SLE (Single Loss Expectancy). Les fréquences anticipées vues précédemment permettent de déterminer l’ARO.

La question que l’on doit se poser c’est si les méthodes vues jusqu’ici, dites objectives, permettent de faire une estimation exacte. Et jusqu’à quel point l’estimation est vraiment objective ? La réponse est clairement que l’estimation des incidents cyber n’est jamais complètement objective, car elle repose sur les perceptions d’un certain nombre de personnes, à commencer par l’analyse de risque, mais toutes les parties prenantes peuvent ajouter des biais et des inexactitudes qu’il sera difficile d’éliminer totalement.
Voici un exemple qui m’est arrivé par le passé. Réalisant une veille d’anticipation des menaces pour une entreprise, j’ai introduit le déni de service dans la liste des possibilités. Je disposais d’un grand nombre de sources externes concordantes pour me rassurer sur la pertinence à la fois de ce choix, mais aussi des statistiques (donc des fréquences) de ces attaques, leur magnitude par pays ou région géographique. Cependant, malgré tous ces éléments, le RSSI ne voulait pas en entendre parler. Il soutenait que le déni de service n’était pas pertinent et que même si cela risquait de se produire, il n’aurait aucun impact significatif pour l’organisation. Sur quelles données s’appuyait-il pour dire cela ? Aucune. Juste le sentiment, la fausse certitude, de disposer des meilleures informations possibles de manière parfaitement arbitraire.
Dans ce cas, qu’est-ce qu’il faudrait retenir : les choix informés avec des données à l’appui comme toute démarche rationnelle commanderait ou bien le sentiment d’un professionnel de la sécurité qui semblait arbitraire ? La réponse est bien souvent politique. C’est la raison pour laquelle, il faut sensibiliser tous les professionnels impliqués directement ou indirectement dans la gestion des risques, et la nécessité d’avoir une démarche rationnelle pltôt que spéculative. Cette démarche nous impose de collecter des données de qualité et en quantité suffisantes avant de tirer la moindre conclusion. Mais aussi d’éliminer les nombreux biais cognitifs qui nous empêchent de voir clair. Malheureusement, ce type de démarche doit s’apprendre, elle n’est pas innée. Et comme tout apprentissage, cela demande d’y consacrer du temps et aussi d’avoir conscience de nos limites pour chercher la remédiation adéquate. C’est toute une culture qu’il faut mettre en place progressivement.

Du fait du grand nombre de paramètres incertains et si la quantité ou la qualité des données sont insuffisantes, les méthodes objectives appliqués aux événements intentionnels ne nous sont pas d’un grand secours. Il faudrait disposer d’un très grand nombre de données et même si c’était le cas, les probabilités usuelles ne s’appliquent pas vraiment aux événements intentionnels complexes qui ont un niveau variable de dépendance entre eux. Pourquoi ?

Voici les difficultés rencontrées :

• Les attaques cyber ont pour origine une décision à un moment donnée de la part d’un acteur de passer à l’acte selon des paramètres insuffisamment compris les rendant très incertains à défaut d’être aléatoires ;
• Les attaques cyber qui comptent, celles qui ont un impact significatif, sont des événements complexes, c’est-à-dire qu’ils se composent d’un grand nombre de variables soit inconnues, soit méconnues et d’événements interreliés ;
• Les attaques cyber impactantes suivent une stratégie constituée des objectifs stratégiques de l’acteur qu’on ne connaît pas à l’avance, eux-mêmes nécessitant d’atteindre au préalable un certain nombre d’objectifs tactiques qui eux dépendent grandement du niveau de résistance rencontré ;
• Puis il est fort à parier que l’organisation va réagir d’une certaine façon lors du premier événement, ce qui va considérablement modifier les paramètres applicables au suivant, elle ne va pas regarder sans rien faire et rester la proie béate aux attaques ultérieures identiques. Si l’organisation est un minimum efficace, elle va modifier ses capacités de prévention, de détection, et de réaction pour tout événement similaire au premier ;
• En outre, parce que les mesures de contrôle du risque sont rarement spécifiques à un événement de menace (par exemple le contrôle d’accès), la modification des capacités pour un événement risque fort de modifier les probabilités qu’un autre événement même différent se produise.

Probabilités bayésiennes

Comment fait-on pour estimer les probabilités d’événements complexes dont les paramètres eux-mêmes sont incertains ? C’est là que les méthodes bayésiennes sont d’un précieux secours. Dans les probabilités bayésiennes, la probabilité est « une mesure du degré de croyance ou de confiance associées avec l’occurrence d’un événement ».
Ces méthodes sont particulièrement adaptées à l’évaluation des risques lorsque les événements dépendent de plusieurs variables partiellement connues (probabilités conditionnelles), dont les observateurs possèdent une croyance particulière que vous avez besoin d’actualiser en continu, et que les probabilités a posteriori dépendent des probabilités a priori … comme c’est le cas lorsque l’évaluation dépend de facteurs tels que le niveau de vulnérabilité (les faiblesses observées) et le degré de résistance face aux événements (les mesures de contrôle implémentées) qu’on veut comparer au niveau de risque inhérent précédemment évalué. Elles permettent d’évaluer, par exemple, la croyance a priori (ou inhérente) puis la croyance a posteriori (ou résiduelle) après avoir évalué la présence et l’efficacité des mesures de contrôle.

Les arbres bayésiens nous permettent également de déterminer des événements complexes ayant des issues de probabilité variable … et ça c’est génial à mon avis, car cela résout les limitations associées aux évaluations de risque traditionnelles qui touchent des événements très (trop) simples, les excluant de fait, alors qu’ils sont la plupart du temps complémentaires.

Exemple d’évaluation du risque associé à la modélisation d’une attaque complexe

Ci-dessous un exemple de modélisation d’une attaque complexe (un rançongiciel) dont on suppose que l’on ait d’abord réalisé une évaluation de chacune des phases pour déterminer le niveau inhérent (à moins de disposer déjà de cette estimation). Ensuite, on détermine le niveau de probabilité pour chacune des étapes une fois considéré la présence de mesures d’atténuation standard attendues pour chacune de ces étapes et on calcule la probabilité agrégée en multipliant toutes les valeurs. Ce type d’estimation tient compte du degré de complexité de ce type d’attaques, ce qui les rendrait moins fréquentes. Une attaque pa rançongiciel de ce type aurait (les valeurs attribuées sont arbitraires) une probabilité de 7,96%. Mais pour obtenir le risque résiduel, il faut aussi déterminer la magnitude d’impact, de préférence en dollars sonnants et trébuchants.

 Pour voir les explications sur la modélisation maison adaptée à la fois de la cyber et de MITRE Att&ck, vous pouvez lire l’article suivant : https://cyriskintel.com/menaces/

Évaluation du niveau de risque par des probabilités bayésiennes

Établissons une hypothèse à étudier : « Quel est la probabilité qu’un attaquant passe le périmètre en contournant le pare-feu sur Internet ? ».

P(A) désignerait la probabilité qu’un événement soit validé comme un incident (attaque réelle) en se basant sur les constats de l’équipe de SOC de l’organisation.

P(B) désignerait la probabilité qu’un tel événement soit détecté à temps a priori, grâce au SIEM dont il faudra ensuite évaluer l’efficacité.

P(A|B) désignerait la probabilité qu’un événement de détection B soit effectivement une attaque confirmée (événement A).

P(B|A) désignerait la probabilité qu’une attaque confirmée A ne soit pas détectée et que l’attaquant aurait contourné les règles du pare-feu à cause. C’est l’étape durant laquelle il faut mesurer le niveau de vulnérabilité (ou susceptibilité selon FAIR).

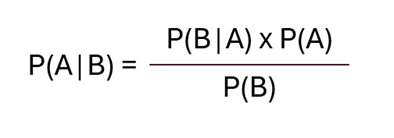
Pour illustrer l’exemple, les équipes du SOC sont assez sûres de n’avoir détecté que peu de contournements de ce pare-feu : P(A) = 0,1 ou 10%.

Après avoir étudié l’implémentation du pare-feu, il s’est avéré que certaines règles n’étaient pas journalisées concernant des protocoles connus pour être exploitables. La probabilité de détecter une violation de la politique de sécurité dans ce pare-feu est estimée à : P(B) = 0,2 ou 20%. Cette probabilité concerne la simple détection de tentatives d’intrusion, pas forcément des attaques réussies et caractérisées.

Par ailleurs, les équipes d’administration des pares-feux sont sous l’eau et elles ont rarement l’occasion de vérifier que tous les flux autorisés sont encore justifiés. Et il apparaîtrait qu’il subsiste certaines vulnérabilités dans ce pare-feu, toujours pas corrigées, permettant à l’attaquant de potentiellement contourner les règles : P(B|A) = 0,8 ou 80%.

La formule bayésienne pour tenir compte de ces estimations serait :

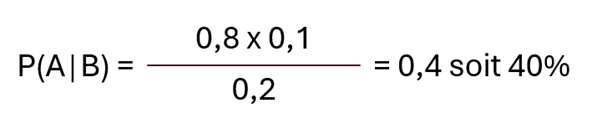
En calculant la valeur d’ALE, on se rend compte que le coût d’un tel événement serait au-delà de la tolérance de l’entreprise qui mandate l’équipe de sécurité pour trouver des mesures d’atténuation du risque nécessitant de diminuer aussi bien l’impact potentiel (les pertes envisagées) en améliorant les mesures réactives ainsi que les probabilités en améliorant la prévention de ce type d’attaque. Les experts décident donc d’améliorer le processus de surveillance, notamment la journalisation et l’alertage, de créer un nouveau cas d’usage permettant au SIEM de mieux intégrer les données issues de la journalisation de ce pare-feu, cela pour diminuer la magnitude d’impact. En même temps, ils décident de créer un projet consistant à passer en revue avec les secteurs d’affaires concernés toutes les règles pour vérifier qu’elles sont toujours nécessaires. Un autre projet est lancé pour corriger la vulnérabilité du pare-feu dans les plus brefs délais.

On demande à l’équipe de réévaluer le risque en tenant compte de ces nouvelles informations. Les analystes reviennent avec l’évaluation suivante :

Les probabilités issues des détections courantes par les équipes du SOC ne changent pas : P(A) = 0,1 ou 10%.

La probabilité de détecter et empêcher une violation de la politique de sécurité dans ce pare-feu est maintenant estimée à : P(B) = 0,05 ou 5%.

La possibilité de contourner le pare-feu et de traverser le périmètre est maintenant estimée : P(B|A) = 0,1 ou 10%.

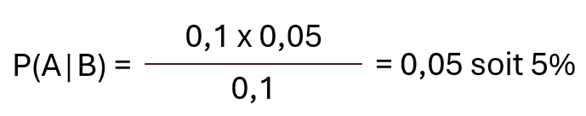
En appliquant cette probabilité à la formule d’ALE précédente, la magnitude d’impact a diminué sous l’action de l’amélioration du processus de détection et la quantité de perte envisagée est maintenant considérée comme acceptable et sous contrôle. L’équipe de surveillance de risque de la deuxième ligne de défense vient confirmer que l’estimation entre maintenant dans les limites définies de l’appétit au risque, qui peut maintenant être accepté.

Vous avez apprécié l’article, avez des suggestions pour l’améliorer, ou vous voudrez que je clarifie un point sur la gestion des risques : vous pouvez me contacter sur LinkedIn ou laisser un commentaire.

Igor S., CISSP, CRISC, FAIR, ISO 27001 LI, etc.